学生実験の内容をまとめました。
使った器具は以下の4つ。
- ファンクションジェネレータ(任意の波形の電気信号を作る機械)
- デジタルオシロスコープ(電圧などの波形を測定する機械)
- BNC-BNC同軸ケーブル
- 50Ω通過型終端抵抗器
接続の基礎
内容
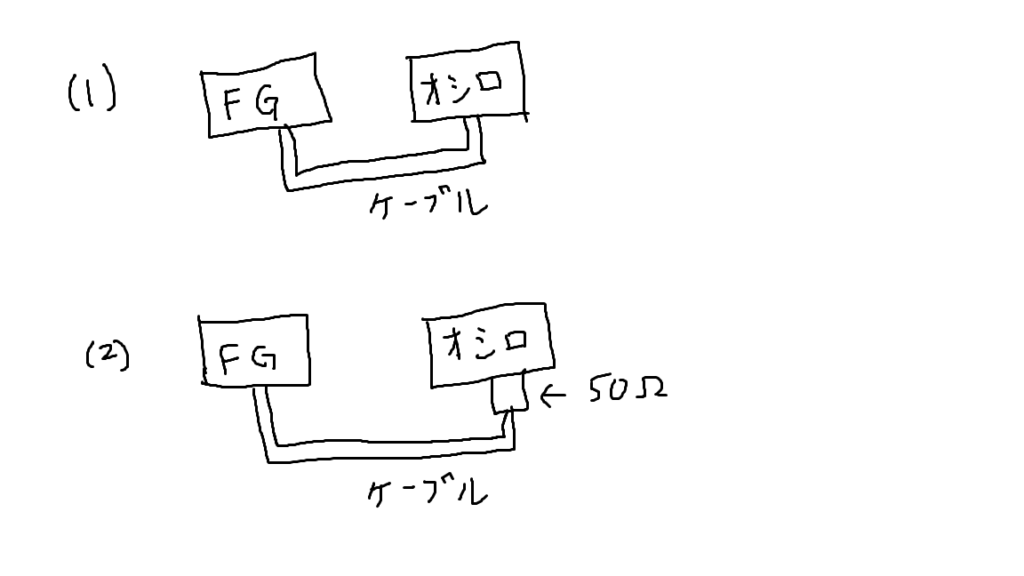
ファンクションジェネレータ(FG)でVpp1Vの正弦波を出力し、ケーブルを通してオシロスコープに入力して振幅を観察しました。
(1)ケーブルとオシロを直接つなぐ場合、(2)ケーブルとオシロの間に50Ω通過型終端抵抗器をはさむ場合、の2パターンで測定しました。
結果
(1)のときVppは2.05V、(2)のときは0.5Vでした。
つまり、(1)ではFGの設定の2倍が、(2)では設定通りの振幅が測定されました。
考察
直接つないだ(1)ではFGの設定の2倍で、抵抗をはさんだ(2)では設定通りだったのはなぜか、の解説です。
理由は、FGの内部抵抗が50Ωで想定されている負荷抵抗が50Ωだったことと、オシロの終端抵抗が1MΩだったことです。要するに、使った機器の仕様。
FGの内部抵抗は50Ωで、つなぐ抵抗が50Ωのときに設定通りの振幅が出るような設計になっています。つまり、FGの電源では設定の2倍の電圧を出しています。
しかし(1)の回路だと、電源で発生した電圧のほとんどがオシロの1MΩの抵抗に加わります。よって(1)の回路では設定の2倍の電圧が測定されました。
(2)で使った通過型終端抵抗器には、以下のような回路図が描かれたシールが貼ってあります。このシールから、つないだケーブルの間に50Ωの抵抗を並列にはさむものだと分かります。
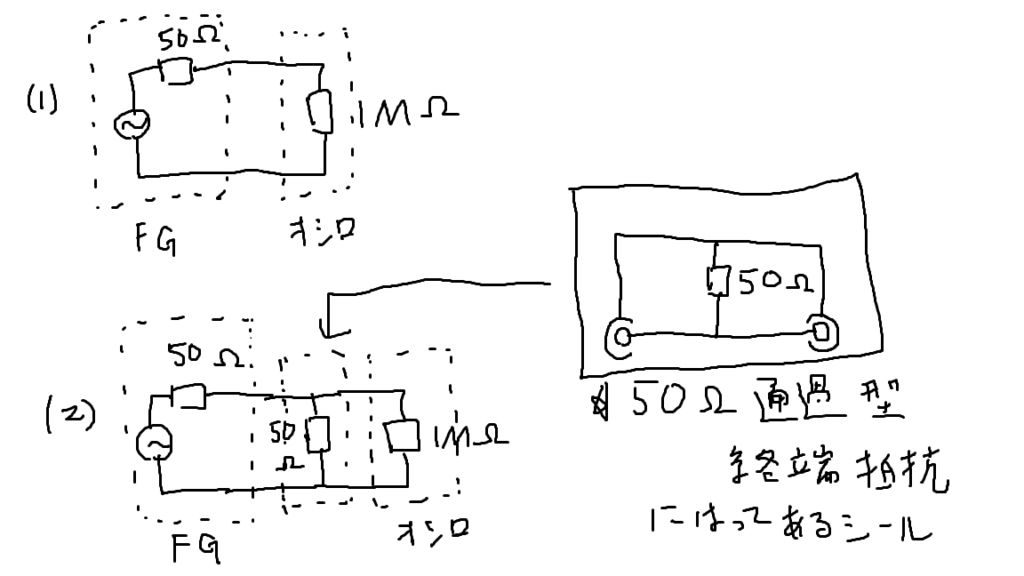
よって(2)の回路ではオシロの1MΩ抵抗にはほとんど電流が流れません。そしてFGの電源電圧は、FGの内部抵抗50Ωと通過型抵抗50Ωでほぼ均等に加わります。その結果オシロでは電源電圧の2分の1、つまりFGの設定通りの電圧が測定されました。

機器の仕様を理解せずに実験をすると、(1)のように想定通りの結果が出られないことがあるよ。気をつけよう!

以下の実験では実験1(2)とおなじ接続をしたよっ
方形波の周波数軸観測
内容
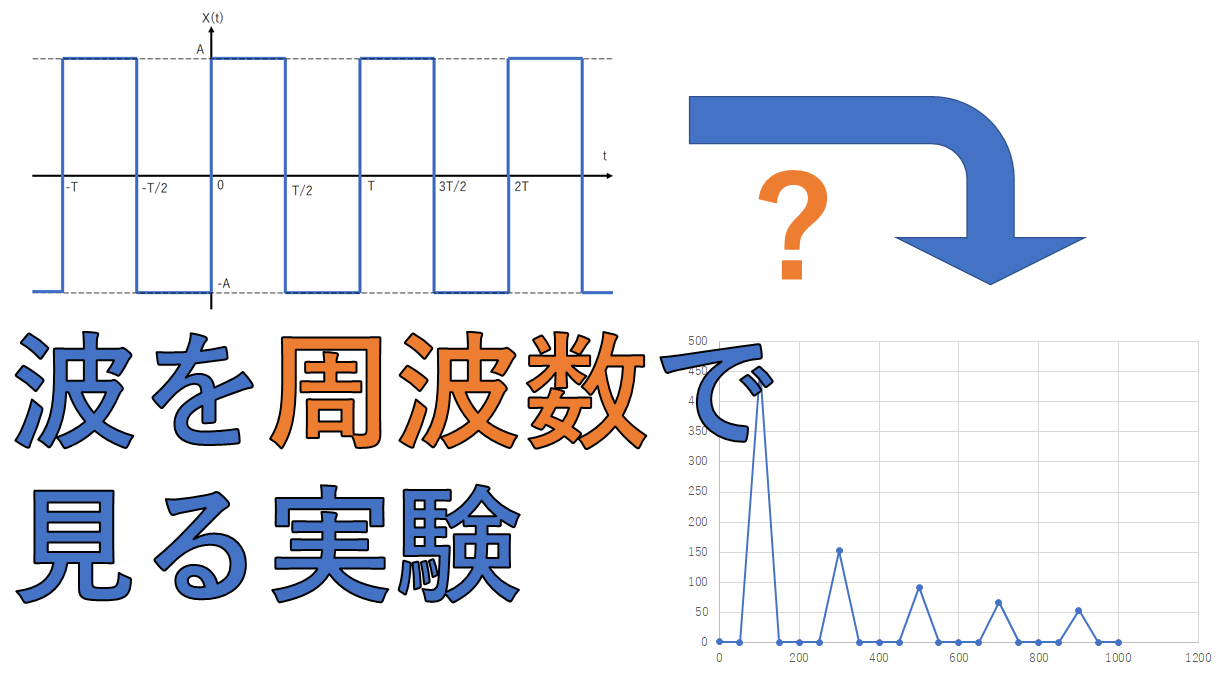
FGで次のような方形波を出力して、オシロのFFT演算機能を使って周波数軸信号について測定しました。
- Vppは1V
- 周波数は100kHz
- デューティー比は50%
下図でA=0.5V、T=10μsとした電圧波形の周波数成分を測定しました。


デューティー比とは、全体の周期に対するONの時間(電圧が高い時間)の割合だよ

FFT(Fast Fourier Transform)とは、測定した信号の周波数成分を求める計算方法だよ
結果
測定した周波数成分ごとの振幅です。
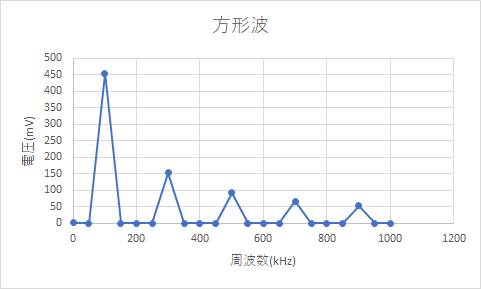
周波数が100×奇数kHzのときだけ電圧が出ていることがわかります。
考察
理由は、周波数がf、振幅がAの方形波をフーリエ変換すると次式のようになるからです。
$$\frac {4}{\pi A}\sum_{n=0}^{\infty }{\frac {1}{2n+1}\sin \{2\pi (2n+1)ft\}}$$
この式のsinの中に$2\pi (2n+1)ft$とあります。この部分から、方形波はfの奇数倍の周波数成分しか持たないことが分かります。
方形波(デューティー比80%)
内容
デューティー比80%の方形波で同じ測定。
次のような波です。

結果
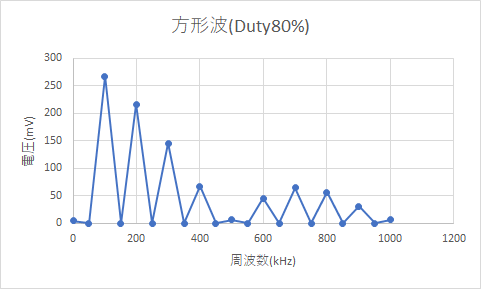
周波数が500k、1000kHzの成分の振幅が、ほかの100kHzの整数倍の周波数成分よりも小さいです。
考察
周波数f、振幅A、デューティー比80%の方形波のフーリエ変換は次式です。
$$\sum_{n=0}^{\infty}{\frac{4A}{\pi n}\sin \frac{4\pi n}{5}\cos 2\pi nft}$$
cosの中身から、fの整数倍の周波数成分を持ちます。しかしsinから、nが5の倍数のとき、すなわちf×(5の倍数)の周波数では振幅が0になることがわかります。
三角波
内容
三角波について同じ測定。

結果

100kと300kHzでは振幅が比較的おおきいですが、ほかは0に近いですね。
考察
周波数f、振幅Aの三角波フーリエ変換は次式になります。
$$\frac {8A}{\pi ^2}\sum_{n=0}^{\infty }{\frac {1}{(2n+1)^2}\cos \{2\pi (2n+1)ft\}}$$
cosの中身から、fの奇数倍の周波数のみを持つことがわかります。また、振幅を表す部分の分母にnの2乗が入っています。ここから、nが大きくなったときの振幅の減衰がはやいことがわかります。
まとめ
- 実験器具にも内部抵抗がある!
- 波をフーリエ変換すると周波数成分がわかる!
つづくー。


コメント