2021/06/10の勉強記録です。
動的計画法というアルゴリズム、計算機の除算と小数点表示についてです。
最短路問題
動的計画法
動的計画法は、「a地点からc地点を経由してb地点まで行く最短の経路は、a→c間の最短路とc→b間の最短路を通ればいい」みたいな考え方で最短路を求める方法です。
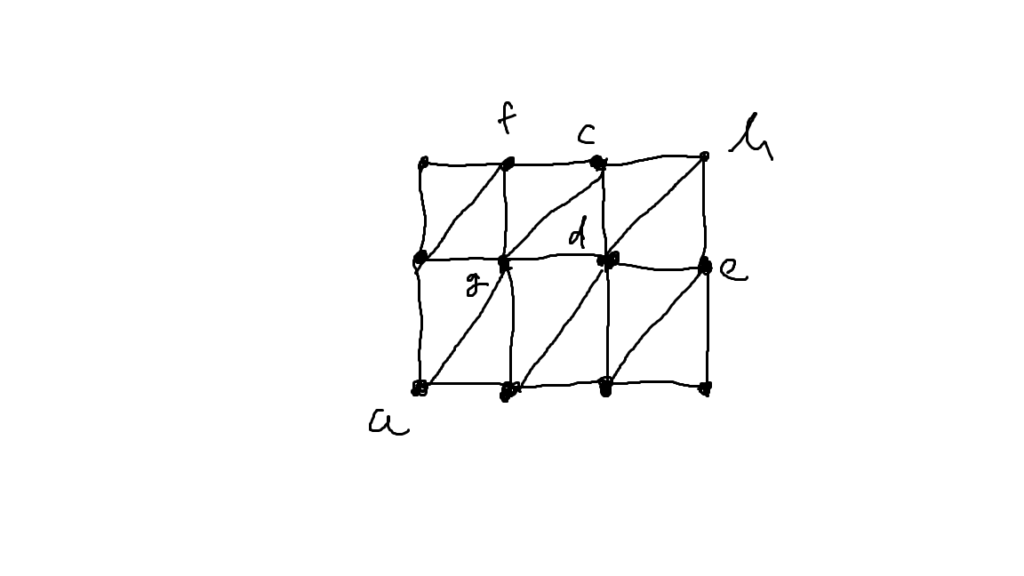
上の図中のa市からb市までの最短経路を求めるとします。
b市にはc村,d村,e村から直接いけるとした場合、
- acの最短経路+bc
- adの最短経路+bd
- aeの最短経路+be
のうち、いちばん短い道を選べばいいわけです。
さらにacの最短経路は
- adの最短経路+dc
- afの最短経路+fc
- agの最短経路+gc
のうちいちばん短い道で…というように、おおきい区間の最短路を求めるために、小さい区間の最短路を求めていきます。
弾性マッチング
さらに、動的計画法の応用として、コスト最小弾性マッチングがあります。
コスト最小弾性マッチングは、パターン認識などに使われます。
パターン認識は、認識したいデータと(多数の)サンプルデータを比べて、一番近いサンプルデータを選びます。
この「一番近い」を判断するための認識データとサンプルデータの「違い」を求めるために、動的計画法を使います。
計算機
除算
人間が筆算などでやるわり算を、どうやって計算機に行わせるか、という話です。
たとえばA=1010,B=10としてA÷Bを求めるとします。
このA,Bは2進数です。
まずAの上1桁「1」に対して、Bとの大小を比べます。
Bのほうが小さいので、商の上1桁目は0です。
次にAの上2桁「10」に対して、Bとの大小を比べます。
「10」=Bのなので、商の上2桁目は1です。
また、R=「10」-Bの計算をしておきます。ここではR=0です。
最後に、Rとの上3桁目をくっつけた「00」とBを比べます。
Bのほうが大きいので、商の3桁目は0です。
A÷Bの結果は「010」です。
ということを言語化します。
固定小数点表示
数字表現に8ビットが与えられたときに、たとえば
「整数部分に4ビット、小数点以下に4ビット」
というように、整数と小数桁を決めておくことを固定小数点表示と言います。
この例だと、8ビット列の4桁目と5桁目の間に小数点が固定されています。
浮動小数点表示
小数を
$$\pm 1.○○ \times 2^n$$
の形で表します。
例えば、符号(\(\pm\))に1桁、指数(\(n\))に8桁、仮数(○○)に23桁、といった感じです。
おわりー。



コメント